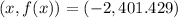Answer:
The absolute extrema of the function
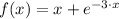 on the domain
on the domain
![[-2,2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/320z36wpj98iz61qegex7j93ut2loj6qfh.png) are:
are:
Absolute minimum:
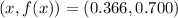
Absolute maximum:
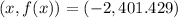
Explanation:
Let
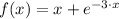 with interval in
with interval in
![[-2,2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/320z36wpj98iz61qegex7j93ut2loj6qfh.png) , we can check if the absolute extrema exist by applying First and Second Derivative Test, otherwise we must evaluate the function at lower and upper bounds.
, we can check if the absolute extrema exist by applying First and Second Derivative Test, otherwise we must evaluate the function at lower and upper bounds.
First, we obtain the first derivative of the function, which is later equalized to zero and solved for
 :
:

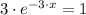


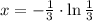

Second, we evaluated the second derivative of given function at result above:
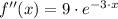
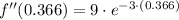
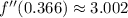 (Absolute minimum)
(Absolute minimum)
The value of the absolute minimum is:
x = 0.366
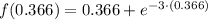
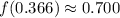
Third, we evaluate the function at each bound in the search for absolute maximum:
x = -2
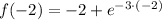
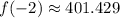
x = 2
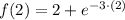
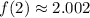
The absolute extrema of the function
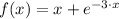 on the domain
on the domain
![[-2,2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/320z36wpj98iz61qegex7j93ut2loj6qfh.png) are:
are:
Absolute minimum:
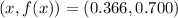
Absolute maximum: