Answer:
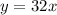
The rate is 224 ft/s
Explanation:
Solving (a):
Given
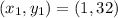
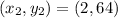
Required
Determine the linear equation
First, we need to determine the slope using

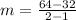
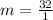
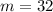
The equation is then calculated using:
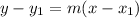
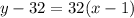
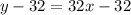
Add 32 to both sides

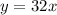
Solving (b):
Given
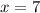
Required
Determine y
We have that:
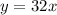
Substitute 7 for x
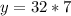
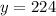
Hence, the rate is 224 ft/s