Complete Question
According to the website for the Balloon Federation of America*, one of the competitive games for the 2014 US Nationals was the "minimum distance double drop". In this event, the balloonist makes a fly in above a marked area on the ground and then tosses out a bean-bag marker into the target. The catch is that the minimum height of the balloon is 1.5 km. That means that the balloon must NOT descend to an altitude less than 1.5 km. Consider this: A judge on the ground looked up to a balloon at its position for dropping the marker on the target. The judge took a line of sight to the top of the balloon and the angle of elevation was 52.5° The judge then back-tracked a distance of 168 m and then determined that the new angle of elevation to balloon (it had not changed altitude) was 41.2°.How could the judge use this information and some right triangle trigonometry to determine the height of the balloon? Was the height of the balloon within the height restrictions for the contest
Answer:
The height of the balloon is
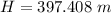
The height of the balloon is not within the restriction
Explanation:
From the question we are told that
The minimum height of the balloon is h = 1.5 km
The angle of elevation is
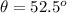
The distance from the position where the marker is dropped is d= 168 m
The angle of elevation at position 168 m from the drop point is
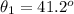
Let the distance of the judge from the balloon at
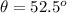 be k m
be k m
Let the height of the balloon from the ground be H
Let the distance of the judge from the balloon at
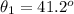 is u = d + k
is u = d + k
So considering the position for dropping the marker , using SOHCAHTOA
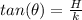
=>
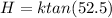
=>
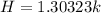
Now considering the position 168 m from the position for dropping the marker , using SOHCAHTOA
at this point altitude has not change so H remains the same
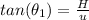
=>

=>
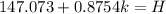
So
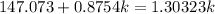
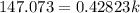
=>
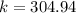
So
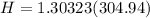
=>
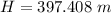
Given that the height obtained is less that 1.5 km then then the height of the balloon is not within the restriction