Answer:
After 1.5 seconds, the rocket will have reached a height of 90 centimeters.
Explanation:
You know that for Jivesh's Model A rocket, he uses the equation:
h = −40*t² + 120*t
You want to know at what time the height of the model A rocket is 90 centimeters, that is, at what time t the height of the rocket h has a value of 90. Substituting this value in the equation you obtain:
90= −40*t² + 120*t
A quadratic equation has the general form:
a*x² + b*x +c= 0
where a, b and c are known values and a cannot be 0.
Taking the equation for Jivesh's model A rocket to that form, you get:
-40*t² +120*t - 90= 0
The roots of a quadratic equation are the values of the unknown that satisfy the equation. And solving a quadratic equation is finding the roots of the equation. For this you use the formula:

In this case, solving the equation is calculating the values of t, that is, you find the moment when the rocket will have reached a height of 90 centimeters.
Being a= -40, b=120 and c= -90, then
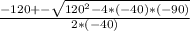
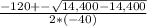
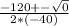
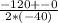
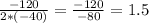
This means that after 1.5 seconds, the rocket will have reached a height of 90 centimeters.