Answer:
1)
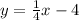
2)
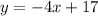
Explanation:
We know that Line A is represented by the equation
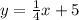 .
.
Notice that the slope of Line A is 1/4.
Part 1) Parallel and Passes Through (8, -2).
Since the new line is parallel, this means that we will have the same slope.
We also know that it passes through (8, -2). So, we can use the point-slope form:
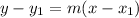
Where m is the slope and (x₁, y₁) is a point.
So, let’s substitute 1/4 for m and (8, -2) for (x₁, y₁), respectively. This yields:
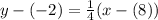
Simplify and distribute the right:
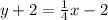
Subtract 2 from both sides. Therefore, our equation in slope-intercept form is:
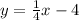
Part 2) Perpendicular and Passes Through (4, 1).
Since the new line is perpendicular, the slope will be the negative reciprocal of the old slope.
To find the negative reciprocal, we flip the number and then multiply it by a negative.
Our old slope is 1/4. Flipping this yields 4/1 or 4. Multiplying by a negative gives us -4.
Therefore, the slope of our new line is -4.
And we also know that it passes through (4, 1).
Again, we can use the point-slope form:
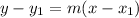
This time, substitute -4 for m and (4, 1) for (x₁, y₁). This yields:
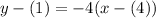
Simplify and distribute:
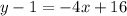
Add 1 to both sides. Therefore, our equation is:
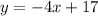
And we are done!