For this case we have the following equation for the volume:
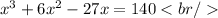
Rewriting the equation we have:
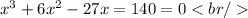
We factor the equation to find the roots of the polynomial.
We have then:
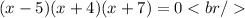
Then, we discard the negative roots, because the dimensions of the figure must be positive.
We have then that the length is:
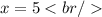
The height is:
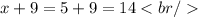
The width is:
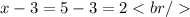
Thus, the dimensions are:
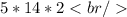
Answer:
The length is 5 inches, the width is 2 inches, and the height is 14 inches.