Answer:
s = 51305.88 m
Step-by-step explanation:
Initial velocity of a rocket, u = 25 mph
We need to find the maximum height of the rocket when it reaches its highest point. At this point, the final velocity of the rocket is equal to 0, v = 0
Using the equation of motion,

Here, a = -g and s is the height reached by rocket
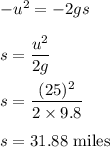
We know that, 1 mile = 1609.34 metre
31.88 miles = 51305.88 m
So, the height reached by the rocket is 51305.88 m.