Question

Write an equation of the perpendicular bisector of the segment with endpoints G(5,-8) and H(7,4) Your answer should be in slope-intercept form. Please type your equation with NO SPACES and if the slope is not a whole number, please make sure it is written as a faction.

Answer 1

`y=-(1)/(6)x-1`

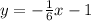
Explanation:

In order to solve this problem we can start by finding the slope of the perpendicular equation. We can do this by finding the slope of the equation that passes through the two points provided by the problem.

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

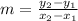
so we input the two points (5,-8) and (7,4) to get:

`m=(4-(-8))/(7-5)`

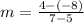
so

m=6

next, we find the negative reciprocal to get the slope of the perpendicular line, so we get:

`m=-(1)/(6)`

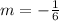
Now we need to find one point that the line passes through.

we can find that point by using the midpoint formula:

`x=(x_(2)+x_(1))/(2)`

`y=(y_(2)+y_(1))/(2)`

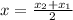
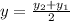
so we get:

`x=(7+5)/(2)=6`

`y=(4-8)/(2)=-2`

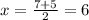
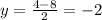
So the point is (6,-2)

So now we can find the equation of the line by using the point-slope form of the linear equation:

`y-y_(1)=m(x-x_(1))`

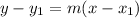
and substitute the point and the slope into the equation:

`y-(-2)=-(1)/(6)(x-6)`

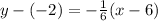
and solve for y:

`y=-(1)/(6)x+1-2`

`y=-(1)/(6)x-1`

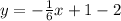
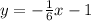
which will be our answer.