Question

Brenda is driving a car going 25 m/s suddenly sees the lights of an intersection 40.0 m ahead. It takes her 0.65 s before she applies the brakes. Once she does begin to brake, her acceleration is at a rate of -25.0 m/s2. Calculate distance traveled before hitting the brakes. A pedestrian is walking in the intersection ahead. Does Brenda hit the pedestrian walking the intersection ahead? Calculate the final velocity and explain.

Answer 1

The car would not hit the pedestrian walking the intersection ahead, as it stops 11.25 meters behind the pedestrian walking the intersection ahead.

Step-by-step explanation:

a) Calculate distance travelled before hitting the brakes

After a careful reading of statement, we notice that car travels at constant velocity before hitting the brakes. Let suppose that Brenda's car has an initial position of zero. The kinematic equation that describes the final position of the car (
`x`), measured in meters, is:

`x = x_(o)+v_(o)\cdot t` (Eq. 1)

Where:

`x_(o)` - Initial position of the car, measured in meters.

`v_(o)` - Initial velocity of the car, measured in meters per second.

`t` - Time, measured in seconds.

If we know that
`x_(o) = 0\,m`,
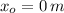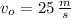`v_(o) = 25\,(m)/(s)` and
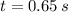`t = 0.65\,s`, the final position of the car is:

`x = 0\,m + \left(25\,(m)/(s)\right)\cdot (0.65\,s)`

`x = 16.25\,m`

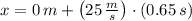
The distance travelled before hitting the brakes is 16.25 meters.

b) Does Brenda hit the pedestrian walking the intersection ahead?

In this stage, Brenda hits the brakes and car decelerates at constant rate, representing a case of uniform accelerated motion. At first we need to confirm if car stopped at a distance behind an intersection, otherwise what velocity Brenda's car had at the moment it passes the intersection. Kinematic formulas are, respectively:

`v^(2) = v_(o)^(2)+2\cdot a\cdot (x-x_(o))` (Eq. 2)

Where:

`v` - Final velocity of the car, measured in meters per second.

`a` - Deceleration of the car, measured in meters per square second.

We proceed to clear final position within equation above:

`x = x_(o)+(v^(2)-v_(o)^(2))/(2\cdot a)`

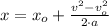
If we know that
`x_(o) = 16.25\,m`,
`a = -25\,(m)/(s^(2))`,
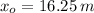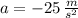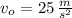`v_(o) = 25\,(m)/(s^(2))` and
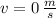`v = 0\,(m)/(s)`, the final position of the car is:

`x = 16.25\,m +(\left(0\,(m)/(s) \right)^(2)-\left(25\,(m)/(s) \right)^(2))/(2\cdot \left(-25\,(m)/(s^(2)) \right))`

`x = 28.75\,m`

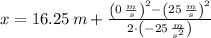
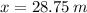
The car would not hit the pedestrian walking the intersection ahead, as it stops 11.25 meters behind the pedestrian walking the intersection ahead.