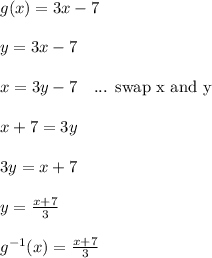Question

Let


`f(x) = √(x + 2) for x \geqslant - 2`

`g(x) = 3x - 7 \: for \: all \: real \: numbers`

`f(x) = √(x + 2) for x \geqslant - 2`

`\: and \: g(x) = 3x - 7 \: for \: all \: real \: numbers`[/tex]

please help me!!​

Answer 1

Answers:

• f(14) = 4
• (g o f)(14) = 5
• 
  `g^(-1)(x) = (x+7)/(3)`

===================================================

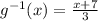
Work Shown:

Plug x = 14 into f(x)

`f(x) = √(x+2)\\\\f(14) = √(14+2)\\\\f(14) = √(16)\\\\f(14) = 4\\\\`

--------------------

Recall that (g o f)(x) is the same as g( f(x) )

This means (g o f)(14) is the same as g( f(14) )

Earlier we found f(14) = 4, so g( f(14) ) = g(4)

Now plug x = 4 into g(x)

`g(x) = 3x-7\\\\g(4) = 3*4-7\\\\g(4) = 12-7\\\\g(4) = 5\\\\`

--------------------

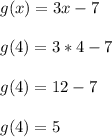
To find the inverse, we swap x and y and solve y like so...

`g(x) = 3x-7\\\\y = 3x-7\\\\x = 3y-7 \ \ \text{ ... swap x and y}\\\\x+7 = 3y\\\\3y = x+7\\\\y = (x+7)/(3)\\\\g^(-1)(x) = (x+7)/(3)\\\\`