Answer:
About 0.054 moles.
Step-by-step explanation:
Apply the ideal gas law. Recall that:
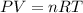
Solve for n, the number of moles:
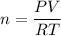
Determine the pressure of the hydrogen gas. Recall that by Dalton's Law of Partial Pressures, the total pressure is equal to the sum of the partial pressures of each individual gas:

Convert the vapor pressure of the liquid to atm (1.00 atm = 760. torr):
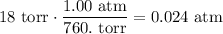
Therefore, the partial pressure of the hydrogen gas is:

Therefore, the number of moles of hydrogen gas present is (the temperature in kelvins is 273.15 + 20.0 = 293.2 K):
