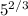Answer:
11.
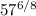
12.
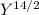
13.
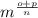
14.
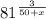
15.
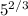
Explanation:
When converting from radicals to rational exponents, there's a quick, easy rule to remember:
The "power" represents the exponent of the radical/radicand, while the "root" represents the index.
11. the eight root of fifty-seven to the sixth degree.
- Write the expression in radical form:
![\sqrt[8]{57^6}](https://img.qammunity.org/2023/formulas/mathematics/college/toc48p5lh6h65ktuwt9682qe69u8ru4zqz.png)
- Rewrite using the exponent rule (power over root):
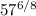
12. the square root of Y to the fourteenth power.
- Write the expression in radical form:
![\sqrt[2]{Y^(14)}](https://img.qammunity.org/2023/formulas/mathematics/college/bdwvlczhjof92edtia6ebf35ln24efmma1.png)
- Rewrite using the exponent rule (power over root):
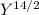
13. the nth root of m to the o plus p degree.
- Write the expression in radical form:
![\sqrt[n]{m^(o+p)}](https://img.qammunity.org/2023/formulas/mathematics/college/7siyvyahznrnkmm4urb739tr1zjxsbsotm.png)
- Rewrite using the exponent rule (power over root):
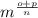
14. The fifth root plus x of eighty-one to the third power.
- Write the expression in radical form:
![\sqrt[5+x]{81^(3)}](https://img.qammunity.org/2023/formulas/mathematics/college/zxurn48uyf5bw7imouzg22nx6f9jppaacw.png)
- Rewrite using the exponent rule (power over root):
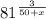
15. The cube root of five squared.
- Write the expression in radical form:
![\sqrt[3]{5^(2)}](https://img.qammunity.org/2023/formulas/mathematics/college/7luqpcv6xyp1649x984axtipwjvsx6lo6w.png)
- Rewrite using the exponent rule (power over root):