
Given :-
•
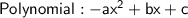
• The zeroes of the given polynomial are α and β .
Let's Begin :-
Here, we have polynomial
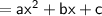
We know that,
Sum of the zeroes of the quadratic polynomial
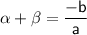
And
Product of zeroes
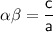
Now, we have to find the polynomials having zeroes :-
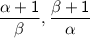
Therefore ,
Sum of the zeroes
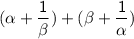
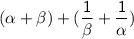

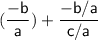
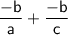
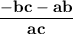
Thus, The sum of the zeroes of the quadratic polynomial are -bc - ab/ac
Now,
Product of zeroes
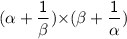
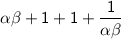

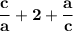
Hence, The product of the zeroes are c/a + a/c + 2 .
We know that,
For any quadratic equation

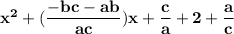
Hence, The polynomial is x² + (-bc-ab/c)x + c/a + a/c + 2 .
Some basic information :-
• Polynomial is algebraic expression which contains coffiecients are variables.
• There are different types of polynomial like linear polynomial , quadratic polynomial , cubic polynomial etc.
• Quadratic polynomials are those polynomials which having highest power of degree as 2 .
• The general form of quadratic equation is ax² + bx + c.
• The quadratic equation can be solved by factorization method, quadratic formula or completing square method.