Using Substitution:
To use substitution to identify if two lines intersect,
1. Rearrange one of the two given equations so that only one variable is on one side of the equation with all other values on the other side of the equation. (if needed)
2. Plug this new equation into the other (in place of a variable)
3. Solve the equation to get the answer of one of the variables
4. Plug this variable into one of the two original equations and solve for the second variable (if needed)
5. Plug both variables back into one of the original equations. If both sides of the equation are equal, the two lines do coincide.
Example:
Equation 1: 2x+3y=9
Equation 2: x+8=3
1. Rearrange equation 2
x+8=3
x=3-8
x=-5
2. Plug -5 into the first equation as x
2x+3y=9
2(-5)+3y=9
3. Solve this equation
-10+3y=9
3y=9+10
3y=19
y=
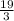
4. Plug x and y back into the first equation
2x+3y=9
2(-5)+3(
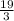 )=9
)=9
-10+19=9
9=9
Therefore, these two lines do coincide. The point of intersection is (-5,
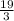 ).
).
Using Elimination:
To use elimination to identify if two lines intersect:
1. Multiply one or both of the equations by a factor so both equations have either an x or y coefficient that are equal or opposite of each other (if needed)
2. Add or subtract the two equations to get rid of one variable
3. Solve this new equation for a variable
4. Substitute this variable into one of the two equations to solve for the other
5. Plug both variables back into one of the equations. If both sides are equal, the two lines do coincide.
Example:
Equation 1: 2x+3y=4
Equation 2: 4x+2y=3
1. For this specific system of equations, we would multiply the first equation by 2.
2x+3y=4
4x+6y=8
Notice how now, both equations have 4x in them, so we can subtract them:
2. Subtract the new equation from the second original equation
4x+6y=8
- 4x+2y=3
4y=5
3. Solve
4y=5
y=

3. Substitute y back into the first equations (any of the two equations will work) to solve for x
2x+3y=4
2x+3(
 )=4
)=4
2x+
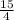 =4
=4
2x=4-
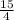
2x=
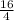 -
-
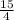
2x=

x=
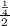
x=

x=

4. Plug both variables back into the first equation (either equation works)
2x+3y=4
2(
 )+3(
)+3(
 )=4
)=4
 +
+
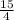 =4
=4
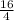 =4
=4
4=4
Since the left side equals the right side, the two lines are coinciding.
Using Graphing Methods:
To use graphing methods to identify if two lines coincide, we would just have to graph the line and identify if the two lines meet at a point of intersection/overlap each other.
I hope this helps!