Answer:
Steps 2 and 3 must be switched.
Explanation:
Let
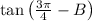 . From Trigonometry we know the following identity:
. From Trigonometry we know the following identity:
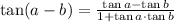 (Eq. 1)
(Eq. 1)
Where
 and
and
 are angles measured in radians.
are angles measured in radians.
Now we proceed to demonstrate the required steps to expand and simplify given expression:
1)
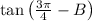 Given.
Given.
2)
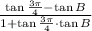
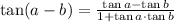 (Step 1)
(Step 1)
3)
 Trigonometric identity. (Step 3)
Trigonometric identity. (Step 3)
4)
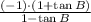 Distributive property/
Distributive property/
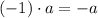 (Step 2)
(Step 2)
5)

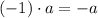 /
/
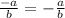 /Result. (Step 4)
/Result. (Step 4)
In a nutshell, steps 2 and 3 must be switched.