Question

Find the equation that is parallel to 2x-y=7

Answer 1

Hi there.

`= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =`

First of all, we can't find the equation of the line that is parallel to the line we are provided with in this problem, which is
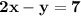`\bf{2x-y=7}`, until we convert this equation into another form.

.

.

This form has a name, and it's called "
`\bf{Slope-Intercept\:Form}`.

.

.

So first, what we need to do is subtract 2x from both sides:

.

`\bf{-y=7-2x}`

.

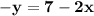
It's not mandatory, but we can re-arrange the terms "7" and "-2x":

.

`\bf{-y=-2x+7}`

.

Last step: Divide both sides of the equation by -1:

.

`\bf{y=2x-7}`

.

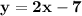
"-2x" turned into "2x" because a negative number multiplied or divided by a negative number equals a positive number.

.

"7" turned into "-7" because a positive number multiplied or divided by a negative number equals a negative number.

.

Now, our equation is in "Slope-Intercept Form".

.

Remember that "Slope-Intercept Form" looks like this:

.

`\bf{y=mx+b}`.

.

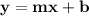Now what we need to find is the equation of the line.

.

Let's skim through the provided information to see whether or not there's some information that can help us find the equation.

.

We're also provided with the fact that these lines, or equations, are parallel.

.

What that means is if two lines are parallel, their slopes are the same.

.

The slope of the line whose equation we just found is -2 (it's the number next to "x").

.

I hope that this helped clear your doubts; if any are left, please ask.

.

I wish you a nice rest of your day.

.

`\bf{W}\sf{r}\bf{i}\sf{t}\bf{i}\sf{n}\bf{g}\:\sf{A}\:\bf{L}\sf{e}\bf{t}\sf{t}\bf{e}\sf{r}.`

--

Answer 2

Below

Explanation:

Lines that are parallel have the same slope, so all lines parallel to the one given have the same slope as it does. That slope value is most easily seen by transforming the given equation to slope-intercept form

(y = mx + b).

This line would be y = 2x -7, so the slope of any line parallel to it must have a slope value of 2.