Question

Solve the following System of equations graphically on the set of axes below

Y= 3/2x -7
Y= -x+3


Please help

Answer 1

(4, -1)

Explanation:

On plotting both functions on a graph, we find that the solution is (4, -1).

Answer 2

(4, -1)

Explanation:

Given equations:

`y=(3)/(2)x-7`

`y=-x+3`

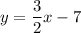
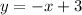
To plot the lines, find 2 points for each equation and draw a straight line through them.

`\textsf{For }\quad y=(3)/(2)x-7:`

`x=0 \implies y=(3)/(2)(0)-7=-7 \implies (0,-7)`

`x=6 \implies y=(3)/(2)(6)-7=2 \implies (6,2)`

`\textsf{For }\quad y=-x+3:`

`x=0 \implies y=-(0)+3=3 \implies (0,3)`

`x=6 \implies y=-(6)+3=-3 \implies (6,-3)`

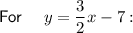
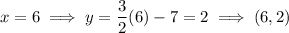
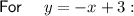
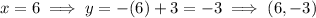
The solution to the system of equations is the point of intersection:

Therefore, from inspection of the graph, the solution is (4, -1)