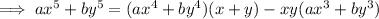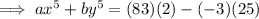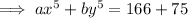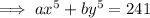Question

Suppose that a, b, x and y are real numbers such that ax+by = 1, ax² + by² = 11, ax³ + by³ = 25 and ax⁴ + by⁴ = 83. Find the value of ax⁵ + by⁵.​

Answer 1

`ax^5+ by^5=241`

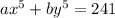
Explanation:

Given:

• 
  `ax + by = 1`
• 
  `ax^2+ by^2 = 11`
• 
  `ax^3+ by^3 = 25`
• 
  `ax^4+ by^4 = 83`

We can re-write the left sides of the given equations as follows:

`ax^2+ by^2=(ax+by)(x+y)-xy(a+b)`

`ax^3+ by^3=(ax^2+by^2)(x+y)-xy(ax+by)`

`ax^4+ by^4=(ax^3+by^3)(x+y)-xy(ax^2+by^2)`

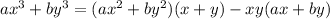
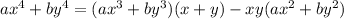
Therefore, following this pattern:

`ax^5+ by^5=(ax^4+by^4)(x+y)-xy(ax^3+by^3)`

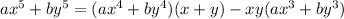
Use the given values and the expanded expressions to create 2 equations to help find the values of (x+y) and xy:

Equation 1

`ax^3+ by^3=(ax^2+by^2)(x+y)-xy(ax+by)`

`\implies 25=11(x+y)-xy(1)`

`\implies 25=11(x+y)-xy`

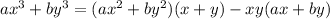
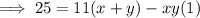
Equation 2

`ax^4+ by^4=(ax^3+by^3)(x+y)-xy(ax^2+by^2)`

`\implies 83=25(x+y)-xy(11)`

`\implies 83=25(x+y)-11xy`

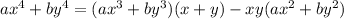
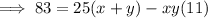
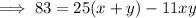
Multiply Equation 1 by 11:

`\implies 275=121(x+y)-11xy`

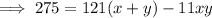
Then subtract Equation 2 from this to eliminate 11xy and find the value of (x+y):

`\implies 192=96(x+y)`

`\implies (x+y)=2`

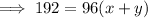
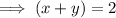
Multiply Equation 1 by 25:

`\implies 625=275(x+y)-25xy`

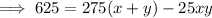
Multiply Equation 2 by 11:

`\implies 913=275(x+y)-121xy`

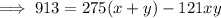
Subtract the 2nd from the 1st to eliminate 275(x+y) and find the value of xy:

`\implies 288=-96xy`

`\implies xy=-3`

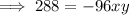
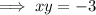
Therefore, we now have:

• 
  `ax^4+ by^4 = 83`
• 
  `ax^3+ by^3 = 25`
• 
  `(x+y)=2`
• 
  `xy=-3`

Substitute these into the equation for ax⁵ + by⁵ and solve:

`\implies ax^5+ by^5=(ax^4+by^4)(x+y)-xy(ax^3+by^3)`

`\implies ax^5+ by^5=(83)(2)-(-3)(25)`

`\implies ax^5+ by^5=166+75`

`\implies ax^5+ by^5=241`