Question

`{\large{\red{\mapsto{\maltese{\underline{\green{\boxed{\blue{\underbrace{\overbrace{\pink{\pmb{\bf{Question:}}}}}}}}}}}}}}`

Factorise using difference of squares method

`\mathsf \blue{2 {a}^(2) - 32}`
​

Answer 1

`\displaystyle 2[a - 4][a + 4]`

Step-by step Step-by-step explanation:

`\displaystyle 2a^2 - 32 \\ 2[a^2 - 16] \\ \\ \boxed{2[a - 4][a + 4]}`

I am joyous to assist you at any time.

Answer 2

`2(a + 4)(a - 4)`

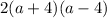
Step-by-step explanations:

• Factorize the expression ( 2a² - 32 ). First, which will give us:

`2( {a}^(2) - 16)`

• But ( a² - 16 ) is a perfect square expression. Therefore it can further be factorized to:

`( {a}^(2) - 16)`

`= (a - 16) ^(2)`

`= (a - 4)(a + 4)`

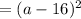
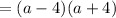
• Hence joining all them will sum up to..:

`2(a - 4)(a + 4)`

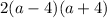
Hope this helps you... :)

#Carry on learning#... :)