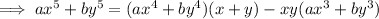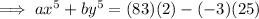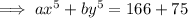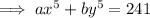Answer:
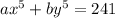
Explanation:
Given:
We can re-write the left sides of the given equations as follows:
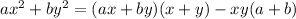
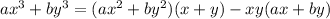
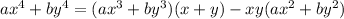
Therefore, following this pattern:
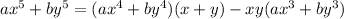
Use the given values and the expanded expressions to create 2 equations to help find the values of (x+y) and xy:
Equation 1
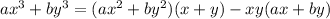
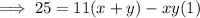
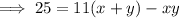
Equation 2
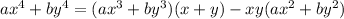
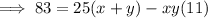
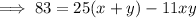
Multiply Equation 1 by 11:
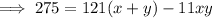
Then subtract Equation 2 from this to eliminate 11xy and find the value of (x+y):
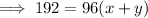
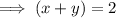
Multiply Equation 1 by 25:
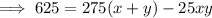
Multiply Equation 2 by 11:
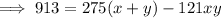
Subtract the 2nd from the 1st to eliminate 275(x+y) and find the value of xy:
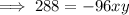
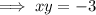
Therefore, we now have:
Substitute these into the equation for ax⁵ + by⁵ and solve: