Solution:
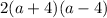
Step-by-step explanations:
• Factorize the expression ( 2a² - 32 ). First, which will give us:
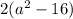
• But ( a² - 16 ) is a perfect square expression. Therefore it can further be factorized to:

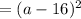
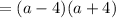
• Hence joining all them will sum up to..:
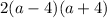
Hope this helps you... :)
#Carry on learning#... :)