Answer:
To find the derivative of
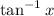 using the first principle of derivative, we need to use the definition of the derivative:
using the first principle of derivative, we need to use the definition of the derivative:
f'(x) = lim(h->0) [(f(x + h) - f(x)) / h]
where f(x) =
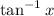 .
.
Substituting f(x) into the definition of the derivative, we get:
f'(x) = lim(h->0) [(
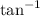 (x + h) -
(x + h) -
![\tan^(-1)/tex) / h]</p><p></p><p>To simplify this expression, we can use the formula for the inverse tangent of a sum:</p><p></p><p>[tex]\tan^(-1)]() (a + b) =
(a + b) =
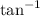 a +
a +
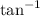 b -
b -
 /2
/2
Using this formula, we can rewrite the numerator of the expression above as:
(
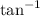 (x + h) -
(x + h) -
![\tan^(-1)/tex) = [tex]\tan^(-1)](https://img.qammunity.org/2023/formulas/mathematics/college/6uiuvybq5ddt0zx00ven04wetglys7i0ng.png) ((x + h) / (1 + (x + h)^2)) -
((x + h) / (1 + (x + h)^2)) -
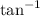 (x / (1 + x^2))
(x / (1 + x^2))
Now, substituting this expression back into the definition of the derivative, we get:
f'(x) = lim(h->0) [
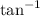 ((x + h) / (1 + (x + h)^2)) -
((x + h) / (1 + (x + h)^2)) -
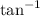 (x / (1 + x^2))] / h
(x / (1 + x^2))] / h
We can simplify this expression using algebra and trigonometry, and we get:
f'(x) = lim(h->0) [h / (1 + x^2 + hx + h^2 + x^2h + xh^2)] / h
f'(x) = lim(h->0) 1 / (1 + x^2 + hx + h^2 + x^2h + xh^2)
Now we can simplify this expression by dropping the terms that contain h^2 or higher powers of h, since they will approach zero faster than h as h approaches zero. We also drop the term containing x^2h, since it is a second-order term and will also approach zero faster than h. This leaves us with:
f'(x) = lim(h->0) 1 / (1 + x^2 + hx)
Now we can evaluate the limit as h approaches zero:
f'(x) = 1 / (1 + x^2)
Therefore, the derivative of
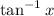 by first principle of derivative is:
by first principle of derivative is:
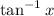 = 1 / (1 + x^2)
= 1 / (1 + x^2)