Answer:
The derivative of the function at
 equals
equals
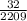 .
.
The equation of the tangent line that passes through the point
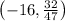 is
is
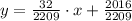 .
.
Explanation:
From Differential Calculus we remember the following definition of derivative,
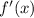 :
:
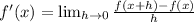 (Eq. 1)
(Eq. 1)
Where
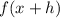 is the function evaluated at
is the function evaluated at
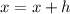 , dimensionless.
, dimensionless.
If we know that
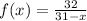 , then
, then
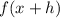 is:
is:
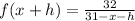 (Eq. 2)
(Eq. 2)
Now we proceed to expand (Eq. 1):
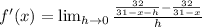 (Eq. 1b)
(Eq. 1b)

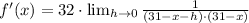
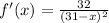 (Eq. 3)
(Eq. 3)
And the derivative is evaluated at
 :
:
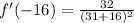
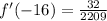
The derivative of the function at
 equals
equals
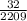 .
.
This value represents the slope of the tangent line that passes through
 , and value of
, and value of
 is now found:
is now found:
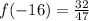
The tangent line is represented by the following model:
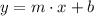 (Eq. 4)
(Eq. 4)
Where:
 - Slope, dimensionless.
- Slope, dimensionless.
 - y-Intercept, dimensionless.
- y-Intercept, dimensionless.
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
If we know that
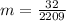 ,
,
 and
and
 , the y-Intercept is:
, the y-Intercept is:
 (Eq. 4b)
(Eq. 4b)
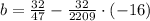
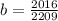
The equation of the tangent line that passes through the point
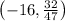 is
is
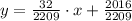 .
.