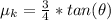Answer:
The value is
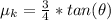
Step-by-step explanation:
Generally the net force acting on the smooth block is mathematically represented as
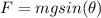
Here this force also represented as
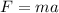
So

=>

Generally from kinematic equation
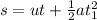
before the sliding the block was at rest so u = 0 m/s
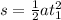
=>

=>
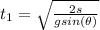
Generally the net force acting on the rough block is mathematically represented as
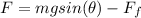
Here
 is the frictional force acting on the block which is mathematically represented as
is the frictional force acting on the block which is mathematically represented as
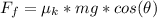
So
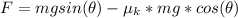
generally this net force is mathematically represented as
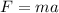
=>

=>
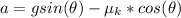
Generally from kinematic equation
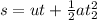
before the sliding the block was at rest so u = 0 m/s
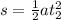
=>
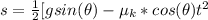
= >
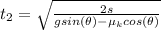
From the question we are told that
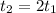
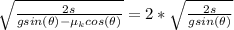
Squaring both sides
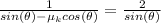
=>
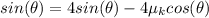
=>
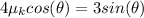
=>
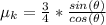
=>