Question

How many one-by-one squares are generated by the algorithm that starts with a single square and on each of its n iterations adds new squares all round the outside. How many one-by-one squares are generated on the nth iteration

Answer 1

Follows are the solution to this question:

Explanation:

please find the complete question in the attached file.

The Pseudocode for Non-Recursive:

In step 1: After completing the Iterations i, the N(i) represent the number of squares.

In step 2: Its pattern of diagonally spaced squares could be found, with alternating lengths.

In step 3: It has runs of the square of length i and i − 1 run of loops of length i − 1. The equation follows:

`N(i) = i 2 + (i -1)2 = 2i \ 2 - 2i + 1.`

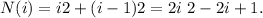
The Pseudocode for the Recursive:

It takes the very same steps and regards it as step 3 instead of step 3 In step 3:

Using the
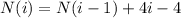`N(i) = N(i -1) + 4i - 4` incidence connection where approximation i square is generated by adding squares arranged in a diamond shape on the other side i. The diamond of length equal to i which consists of 4i − 4 squares.