Question

A 5.00-g bullet comes out a 1.00-kg handgun at a speed of 8.00× 102 m/s when the handgun is held still. What is speed of the bullet if the handgun is held very loosely, assuming that the same amount of kinetic energy is generated each time when the handgun is fired?

Answer 1

The velocity is
`v  = 796 \  m/s`

Step-by-step explanation:

From the question we are told that

The mass of the bullet is
`m_b  =  5.00\  g =  0.005 \ g`

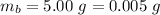
The mass of the hand gun is
`m_g  =  1.00 \ kg`

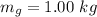
The speed of the gun is
`v_b  =  8.00 * 10^(2) \  m/s`

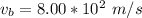
Generally from the law of momentum conservation

`m_b *  u_b  +  m_g *  u_g  =  m_b*  v_b +  m_g *  - v_g`

here
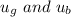`u_g\  and \   u_b` are zero given that before the bullet was shot the gun was at rest

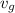`v_g` is negative given because from Newtons third law action and reaction is equal and opposite so if the bullet is moving forward the gun will be moving backward

So

`0.005 *  0  +  1* 0=  0.005 * 8.00 * 10^(2)  -   1.00*  v_g`

=>
`v_g  =  4 \  m/s`

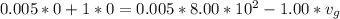
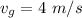
Hence the velocity of the bullet with respect to the loose gun is

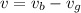
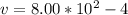
`v  =  v_b  -  v_g`

=>
`v  =  8.00 * 10^(2)   - 4`

=>
`v  = 796 \  m/s`