Question

Calculate the pH in a solution prepared by continuously bubbling SO2 at a pressure of 0.500 atm into pure water.

Answer 1

The pH in a solution prepared by continuously bubbling SO₂ is 1.03.

Step-by-step explanation:

Searching in google the reaction is:

SO₂(g) + H₂O(l) ⇄ H₂SO₃(ac) K = 1.33

The constant is:

`K = \frac{[H_(2)SO_(3)]}{P_{SO_(2)}} = 1.33`

Having that K = 1.33 and P(SO₂) = 0.500 atm, the concentration of H₂SO₃ is:

`[H_(2)SO_(3)] = K*P_{SO_(2)} = 1.33*0.500= 0.665 M`

Now, we have the following dissociation of H₂SO₃ in water:

H₂SO₃(ac) + H₂O(l) ⇄ HSO₃⁻(ac) + H₃O⁺(ac) Ka₁ = 1.5x10⁻²

0.665-x x x

`Ka_(1) = ([HSO_(3)^(-)][H_(3)O^(+)])/([H_(2)SO_(3)]) = 1.5\cdot 10^(-2)`

`1.5\cdot 10^(-2) = (x^(2))/(0.665 - x)`

Solving the above equation for x we have:

x = 0.093 = [H₃O⁺] = [HSO₃⁻]

Also, the HSO₃⁻ dissociates in water as follows:

HSO₃⁻(c) + H₂O(l) ⇄ SO₃²⁻(ac) + H₃O⁺(ac) Ka₂ = 6.3x10⁻⁸

0.093-y y 0.093+y

`Ka_(2) = ([SO_(3)^(2-)][H_(3)O^(+)])/([HSO_(3)^(-)]) = 6.3\cdot 10^(-8)`

`6.3\cdot 10^(-8) = (y(0.093 + y))/((0.093 - y))`

`6.3\cdot 10^(-8)*(0.093 - y) - y(0.093 + y) = 0`

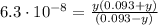
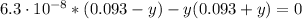
Solving the above equation for y we have:

y = 6.3x10⁻⁸

So, the concentration of H₃O⁺ is:

`[H_(3)O^(+)] = 0.093 M + 6.3\cdot 10^(-8) M = 0.093 M`

Finally, the pH is:

`pH = -log[H_(3)O{+}] = -log(0.093) = 1.03`

Therefore, the pH in a solution prepared by continuously bubbling SO₂ is 1.03.

I hope it helps you!