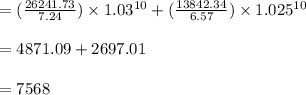Question

Fund A is invested at an effective annual interest rate of 3%. Fund B is invested at an effective annual interest rate of 2.5%. At the end of 20 years, the total in the two funds is 10,000. At the end of 31 years, the amount in Fund A is twice the amount in Fund B. Calculate the total in the two funds at the end of 10 years.

Answer 1

The answer is "7568"

Step-by-step explanation:

It took the funds through account the interest becomes compound. s Lets people, therefore, consider the primary in funds A as PA & the main sum of finances B as PB, the details presented as follows:

We get , and we'll have the P_B value throughout the second equation:

`\to P_A1.03^(31) = 2(10000 - PA1.03^(20))1.025^(11)\\\\\to P_A(1.03^(31) + 2 * 1.03^(20) * 1.025^(11))\\\\ = 20000 * 1.025^(11)\\\\\to P_A = ((20000 * 1.025^(11)))/((1.0331 + 2 * 1.03^(20) * 1.025^(11)))`

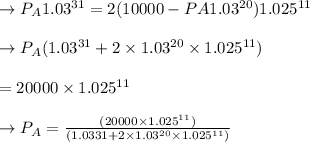
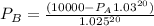`P_B = ((10000 - P_A1.03^(20)))/(1.025^(20))`, So putting in this equation the above
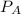`P_A` value

`P_B = \frac{[ {10000 - {(20000 * 1.025^(11))}{(1.03^(31) + 2 * 1.03^(20) * 1.025^(11))}1.03^(20)]}}{1.025^(20)}`

We want to find
`P_A1.03^(10) + P_B1.025^(10)` so we have the last
`P_A \ \& \ P_B` values (in bold)-

`\to ([(20000 * 1.025^(11)))/((1.03^(31) + 2 * 1.03^(20) * 1.025^(11))] * 1.03^(10))`
`+ ((10000 * 1.03^(11)))/((1.03^(11) *1.025^(20)+2 * 1.025^(31)) * 1.025^(10))\\\\`

`=( (26241.73)/(7.24)) * 1.03^(10) + ((13842.34)/(6.57)) * 1.025^(10)\\\\= 4871.09 + 2697.01\\\\ = 7568`