Question

Dora Knob drives her new car off a cliff that is 100 m high. If she lands 33 m away from the base of the cliff, what was her velocity off the cliff

Answer 1

The velocity of Dora Knob's car off the cliff is approximately 36.251 meters per second.

Step-by-step explanation:

According to this situation, Dora Knob starts at a height of 100 meters from rest and lands at a height of 33 meters above the base of the cliff. If we supposed that air friction is negligible, the Principle of Energy Conservation on the car is represented by the following expression:

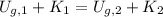`U_(g,1) + K_(1) = U_(g, 2)+K_(2)` (Eq. 1)

Where:

`U_(g,1)`,
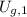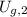`U_(g,2)` - Initial and final gravitational potential energies, measured in joules.

`K_(1)`,
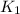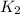`K_(2)` - Initial and final kinetic energies, measured in joules.

The final kinetic energy is now cleared within expression:

`K_(2) = K_(1) + (U_(g,1)-U_(g,2))`

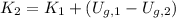
And we expand the expression above by definitions of gravitational potential and kinetic energies:

`(1)/(2)\cdot m \cdot v_(2)^(2) = (1)/(2)\cdot m \cdot v_(1)^(2)+m\cdot g\cdot (z_(1)-z_(2))`

`v_(2)^(2) = v_(1)^(2) + 2\cdot g \cdot (z_(1)-z_(2))`

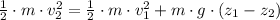
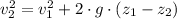
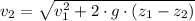`v_(2) = \sqrt{v_(1)^(2)+2\cdot g \cdot (z_(1)-z_(2))}` (Eq. 1b)

Where:

`m` - Mass of the car, measured in kilograms.

`v_(1)`,
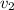`v_(2)` - Initial and final speed of the car, measured in meters per second.

`g` - Gravitational acceleration, measured in meters per square second.

`z_(1)`,
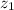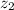`z_(2)` - Initial and final heights of the car above the base of the cliff, measured in meters.

If we know that
`v_(1) = 0\,(m)/(s)`,
`g = 9.807\,(m)/(s^(2))`,
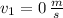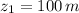`z_(1) = 100\,m` and
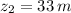`z_(2) = 33\,m`, the velocity of the car off the cliff is:

`v_(2) = \sqrt{\left(0\,(m)/(s) \right)^(2)+2\cdot\left(9.807\,(m)/(s^(2)) \right)\cdot (100\,m-33\,m) }`

`v_(2) \approx 36.251\,(m)/(s)`

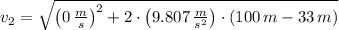
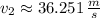
The velocity of Dora Knob's car off the cliff is approximately 36.251 meters per second.