Answer:
The friction factor
 is approximately 0.0179.
is approximately 0.0179.
Step-by-step explanation:
At first we need to know what flow regime water flow is found in. Reynolds number offers an appropriate dimensionless indicator for flow in pipes and whose formula is:
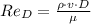 (Eq. 1)
(Eq. 1)
Where:
 - Density of water, measured in kilograms per cubic meter.
- Density of water, measured in kilograms per cubic meter.
 - Dynamic viscosity, measured in kilograms per meter-second.
- Dynamic viscosity, measured in kilograms per meter-second.
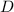 - Inner diameter of pipe, measured in meters.
- Inner diameter of pipe, measured in meters.
 - Flow average speed, measured in meters per second.
- Flow average speed, measured in meters per second.
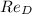 - Reynolds number, dimensionless.
- Reynolds number, dimensionless.
The average speed of water is determined by the following expression:
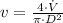 (Eq. 2)
(Eq. 2)
Where:
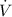 - Volume flow, measured in cubic meters per second.
- Volume flow, measured in cubic meters per second.
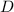 - Inner diameter of pipe, measured in meters.
- Inner diameter of pipe, measured in meters.
If we know that
 and
and
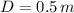 , the flow average speed is:
, the flow average speed is:
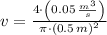

The properties of water at given conditions (
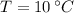 ) are, respectively:
) are, respectively:
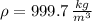
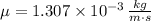
And the Reynolds Number is:
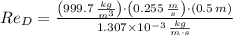
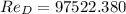
Which means that water is in turbulent flow. There are several empirical and semi-empirical expression to estimate friction factor, we decided to use the Haaland approximation due to its exactness and simplicity:
![(1)/(√(f)) = -1.8\cdot \log_(10)\left[(6.9)/(Re)+\left((\epsilon)/(3.7\cdot D)\right)^(1.11) \right]](https://img.qammunity.org/2021/formulas/engineering/college/iesaztnmxji0ijotmurdvvfnihbb6qvfuy.png) (Eq. 3)
(Eq. 3)
Where:
 - Friction factor, dimensionless.
- Friction factor, dimensionless.
 - Smoothness factor, dimensionless.
- Smoothness factor, dimensionless.
If we know that
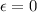 and
and
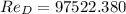 , then we get that:
, then we get that:
![(1)/(√(f))=-1.8\cdot \log_(10)\left[(6.9)/(97522.380) \right]](https://img.qammunity.org/2021/formulas/engineering/college/mvjg9elyvl3o4r24tvy3dlqfyiys9ow2w1.png)
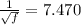
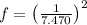
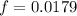
The friction factor
 is approximately 0.0179.
is approximately 0.0179.