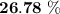Question

A solar-powered steam plant uses a solar collector to heat the water in place of the typical boiler. For a solar-powered steam plant operating on an ideal Rankine cycle, saturated vapor leaves the solar collector at 1 MPa and the pressure in the condenser is 10 kPa. Determine the net work per unit mass and the thermal efficiency of this cycle.

Answer 1

The net work per unit mass
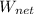`W_(net)` = 692.14 kJ/kg

The thermal efficiency for the cycle =
`\mathbf{26.78 \ \%}}`

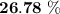
Step-by-step explanation:

For an Ideal Rankine cycle:

The following properties were obtained from the steam tables at 1 MPa.

`h_1 = h_g = 2777.1 \ kJ/kg`

`s_1 = 6.585 \ kJ/kg.k`

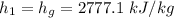
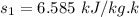
The properties obtained at 10 kPa are:

`h_f = 191.81 \ kJ/kg\\ \\ h_f_g = 2392.1 \ kJ/kg \\ \\ s_f= 0.6492 \ kJ/kg .k \\ \\ s_f_g = 7.4996 \ kJ/kg/k \\ \\ v_f = 0.001010 \ m^3 /kg`

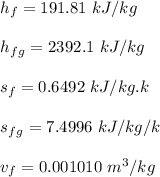
For 1 - 2 isentropic expansion:

`s_1 = s_2`

`s_1 = (s_f+x_2 * 7.4996)`

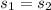
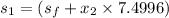
6.585 = 0.6492 + x₂ × 7.4996

6.585 - 0.6492 = 7.4996x₂

5.9358 = 7.4996x₂

x₂ = 5.9358/7.4996

x₂ = 0.791

`h_2 = h_f + x_2 \ hfg`

`h_2 = 191.81 + 0.791 * 2392.1`

`h_2 = 2083.96 \ kJ/kg`

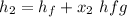
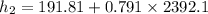
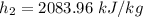
At 10 kPa;

`h_3= h_f = 191.81 \ kJ//kg`

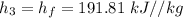
The pump work for the process:

`h_4 - h_3 = vf(\Delta \ P)`

`h_4 - h_3 = 0.001010(1000 -10)`

`h_4 - h_3 = 0.9999 kJ/kg`

`h_4 - 191.81 \ kJ/kg = 0.9999 kJ/kg`

`h_4 = 191.81 \ kJ/kg + 0.9999 kJ/kg`

`h_4 = 192.8 \ kJ/kg`

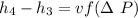
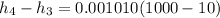
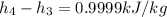
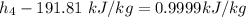
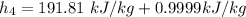
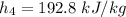
However, the turbine work
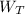`W_T` can be computed by using the formula:

`W_T = h_1 -h_2`

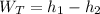
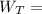`W_T =` ( 2777.1 - 2083.96 ) kJ/kg

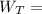`W_T =` 693.14 \ kJ/kg

Thus, the net work
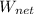`W_(net)` can be determined as:

`W_(net)` =
`W_T - W_p`

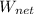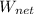`W_(net)` = 693.14 - 0.9999

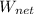`W_(net)` = 692.14 kJ/kg

Similarly, to determine the thermal efficiency of this cycle, we need to first know the heat addition
`Q_s= h_1 - h_4`

`Q_s= (2777.1 -192.8 ) \ kJ/kg`

`Q_s= 2584.3 \ kJ/kg`

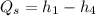
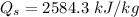
Finally, the thermal efficiency can be calculated by using the formula:

`n_(th) = (W_(net))/(Q_s)`

`n_(th) = (692.14)/(2584.3)`

`n_(th) = 0.2678`

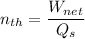
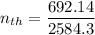
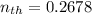
The thermal efficiency for the cycle =
`\mathbf{26.78 \ \%}}`