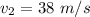Answer:
The velocity of the truck is
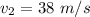
The velocity of the car is
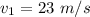
Step-by-step explanation:
From the question we are told that
The natural frequency of a truck horn is
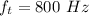
The apparent frequency of the truck horn is
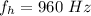
The relative speed is
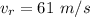
Generally the relative speed when the truck and the car are moving towards each other is
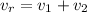
Here
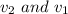 are the velocities of the truck and the car respectively
are the velocities of the truck and the car respectively
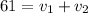
=>
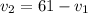
Generally the apparent frequency is mathematically represented as
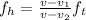
Here v is the speed of sound with value
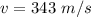
=>
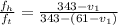
=>
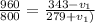
=>
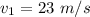
From the above equation we have that
=>
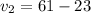
=>