Question

Help ??

(Pls don’t answer unless you know)

Answer 1

Answer:
`\boldsymbol{\left(x, (2)/(3)x-1\right)}`

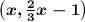
This is the same as writing ( x, (2/3)x-1 )

============================================================

Step-by-step explanation:

The red and green lines are identical. They are drawn very slightly apart so the reader can spot the difference (you'll have to look really closely).

Because both lines are identical, this means we have infinitely many solutions. The two lines intersect at infinitely many locations. Each solution is on that line.

Your teacher wants you to find the equation of this line so you can write all solutions of the form (x, mx+b).

---------

The red line goes through (0,-1) and (3,1). Let's find the slope of this line

m = (y2-y1)/(x2-x1)

m = (1-(-1))/(3-0)

m = (1+1)/(3-0)

m = 2/3

The y intercept is b = -1 because the red line crosses the y axis at this location.

So we go from
`y = mx+b` to
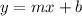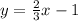`y = (2)/(3)x-1` to represent the equation of both red and green lines.

Any
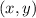`(x,y)` solution on this line is of the form
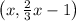`\left(x, (2)/(3)x-1\right)` since we replace y with
`(2)/(3)x-1`

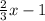
To write
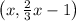`\left(x, (2)/(3)x-1\right)` on a keyboard, you can type ( x, (2/3)x-1 )