Question

The joint probability mass function of XX and YY is given by p(1,1)=0p(2,1)=0.1p(3,1)=0.05p(1,2)=0.05p(2,2)=0.3p(3,2)=0.1p(1,3)=0.05p(2,3)=0.1p(3,3)=0.25 p(1,1)=0p(1,2)=0.05p(1,3)=0.05p(2,1)=0.1p(2,2)=0.3p(2,3)=0.1p(3,1)=0.05p(3,2)=0.1p(3,3)=0.25 (a) Compute the conditional mass function of YY given X=3X=3: P(Y=1|X=3)

Answer 1

P(Y=1|X=3)=0.125

Explanation:

Given :

p(1,1)=0

p(2,1)=0.1

p(3,1)=0.05

p(1,2)=0.05

p(2,2)=0.3

p(3,2)=0.1

p(1,3)=0.05

p(2,3)=0.1

p(3,3)=0.25

Now we are supposed to find the conditional mass function of Y given X=3 : P(Y=1|X=3)

P(X=3) = P(X=3,Y=1)+P(X=3,Y=2) +P(X=3,Y=3)

P(X=3)=p(3,1) +p(3,2) +p(3,3)

P(X=3)=0.05+0.1+0.25=0.4

`P(Y=1|X=3)=(P(X=3,Y=1))/(P(X=3)) =(p(3,1))/(P(X=3))=(0.05)/(0.4)= 0.125`

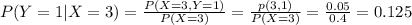
Hence P(Y=1|X=3)=0.125