Question

The height (in meters) of a projectile shot vertically upward from a point 3 m above ground level with an initial velocity of 21.5 m/s is

Answer 1

a) The velocity of the projectile at 2 seconds after launch is 1.9 meters per second. The velocity of the projectile at 4 seconds after launch is -17.7 meters per second.

b) The projectile reaches maximum height 2.192 seconds after launch.

c) The maximum height of the projectile is 26.584 meters above ground.

d) The projectile will hit the ground at 4.523 seconds after launch.

e) The velocity of the projectile right before hitting the ground in -22.871 meters per second.

Step-by-step explanation:

Complete statement of problem is: The height (in meters) of a projectile shot vertically upward from a point 3 m above ground level with an initial velocity of 21.5 meters per second is
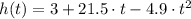`h(t) = 3+21.5\cdot t-4.9\cdot t^(2)`after t seconds. (Round your answers to two decimal places.) (a) Find the velocity after 2 seconds and after 4 seconds, (b) When does the projectile reach its maximum height? (c) What is the maximum height? (d) When does it hit the ground? (e) With what velocity does it hits the ground?

a) From Physics and Differential Calculus we remember that velocity is the first derivative of height. Hence, we need to differentiate the height function in time:

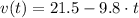`v(t) = 21.5-9.8\cdot t` (Eq. 1)

Where
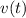`v(t)` is the velocity function, measured in meters per second.

Now we evaluate this function at given times:

t = 2 s.

`v(2) = 21.5-9.8\cdot (2)`

`v(2) = 1.9\,(m)/(s)`

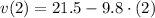
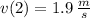
The velocity of the projectile at 2 seconds after launch is 1.9 meters per second.

t = 4 s.

`v(4) = 21.5-9.8\cdot (4)`

`v(4) = -17.7\,(m)/(s)`

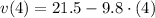
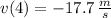
The velocity of the projectile at 4 seconds after launch is -17.7 meters per second.

b) Maximum height is reached when velocity of projectile is zero. We equalize velocity to zero and solve the expression for
`t`:

`21.5-9.81\cdot t = 0`

`t = 2.192\,s`

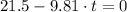
The projectile reaches maximum height 2.192 seconds after launch.

c) Maximum height is calculated by evaluating height function at the time found in b). That is:

`h(2.192) = 3+21.5\cdot (2.192)-4.9\cdot (2.192)^(2)`

`h (2.192) = 26.584\,m`

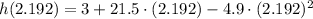
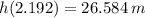
The maximum height of the projectile is 26.584 meters above ground.

d) In this case, we need to equalize the height function to zero and solve for
`t`. That is:

`3+21.5\cdot t-4.9\cdot t^(2) = 0`

Roots are found by means of Quadratic Formula:

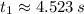`t_(1)\approx 4.523\,s` and
`t_(2)\approx -0.135\,s`

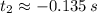
Only the first root offers a physically reasonable solution. Therefore, the projectile will hit the ground at 4.523 seconds after launch.

e) This can be found by evaluating velocity function at the time found in d):

`v(4.523) = 21.5-9.81\cdot (4.523)`

`v(4.523) = -22.871\,(m)/(s)`

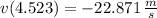
The velocity of the projectile right before hitting the ground in -22.871 meters per second.