Question

The horizontal surface on which the block slides is frictionless. The speed of the block before it touches the spring is 6.0 m/s. How fast is the block moving at the instant the spring has been compressed 15 cm

Answer 1

The final speed of the block moving at the instant the spring has been compressed is approximately 3.674 meters per second.

Step-by-step explanation:

The spring constant is 2000 newtons per meter. Let consider the spring-block system, from Principle of Energy Conservation we can represent it by the following model:

`U_(k,1)+K_(1) = U_(k,2)+K_(2)`

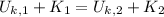
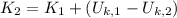`K_(2) = K_(1)+(U_(k,1)-U_(k,2))` (Eq. 1)

Where:

`K_(1)`,
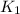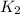`K_(2)` - Initial and final kinetic energies of the block, measured in joules.

`U_(k,1)`,
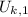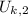`U_(k,2)` - Initial and final elastic potential energy, measured in joules.

And we expand the equation above by definitions of elastic potential energy and kinetic energy:

`(1)/(2)\cdot m \cdot v_(2)^(2) = (1)/(2)\cdot m\cdot v_(1)^(2) + (1)/(2)\cdot k\cdot (x_(1)^(2)-x_(2)^(2))`

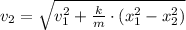`v_(2) = \sqrt{v_(1)^(2)+(k)/(m)\cdot (x_(1)^(2)-x_(2)^(2)) }` (Eq. 1b)

Where:

`m` - Mass of the block, measured in kilograms.

`k` - Spring constant, measured in newtons per meter.

`v_(1)`,
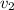`v_(2)` - Initial and final velocities of the block, measured in meters per second.

`x_(1)`,
`x_(2)` - Initial and final positions of spring, measured in meters.

If we know that
`v_(1) = 6\,(m)/(s)`,
`k = 2000\,(N)/(m)`,
`m = 2\,kg`,
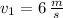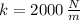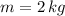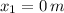`x_(1) = 0\,m` and
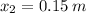`x_(2) = 0.15\,m`, the final speed of the block moving at the instant the spring has been compressed is:

`v_(2) = \sqrt{\left(6\,(m)/(s) \right)^(2)+\left((2000\,(N)/(m) )/(2\,kg) \right)\cdot [(0\,m)^(2)-(0.15\,m)^(2)]}`

`v_(2)\approx 3.674\,(m)/(s)`

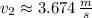
The final speed of the block moving at the instant the spring has been compressed is approximately 3.674 meters per second.