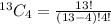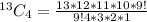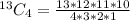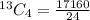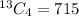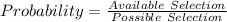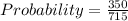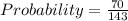Question

There are 55 black balls and 88 red balls in an urn. If 44 balls are drawn without replacement, what is the probability that no more than 11 black ball is drawn

Answer 1

`Probability = (70)/(143)`

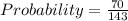
Explanation:

Given

`Black = 5`

`Red = 8`

`Total = 13`

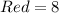
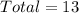
To solve the required probability, we need to determine the number of available selections:

There are two possible scenarios;

1: All 4 selections are red.

2. 1 selection is black, while 3 others are red

Scenario 1: All Red

`^8C_4 = (8!)/((8-4)!4!)`

`^8C_4 = (8!)/(4!4!)`

`^8C_4 = (8*7*6*5*4!)/(4!4!)`

`^8C_4 = (8*7*6*5)/(4!)`

`^8C_4 = (8*7*6*5)/(4*3*2*1)`

`^8C_4 = (1680)/(24)`

`^8C_4 = 70`

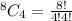
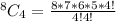
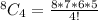
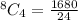
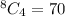
Scenario 2: 1 Black, 3 Red

Selecting Black:

`^5C_1 = (5!)/((5-1)!1!)`

`^5C_1 = (5!)/(4!1!)`

`^5C_1 = (5*4!)/(4!*1)`

`^5C_1 = 5`

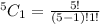
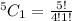
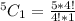
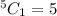
Selecting Red:

`^8C_3 = (8!)/((8-3)!3!)`

`^8C_3 = (8!)/(5!3!)`

`^8C_3 = (8*7*6*5!)/(5!3*2*1)`

`^8C_3 = (8*7*6)/(6)`

`^8C_3 = 8*7`

`^8C_3 = 56`

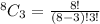
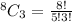
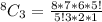
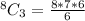
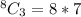
Number of Selection = 5 * 56

`Selection = 280`

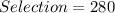
Total Available Selection is calculated as thus:

`Available\ Selection = 70 + 280`

`Available\ Selection= 350`

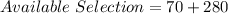
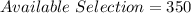
Next, is to calculate the number of possible selections:

i.e 4 balls out of 13

This is calculated as:

`^(13)C_4 = (13!)/((13-4)!4!)`

`^(13)C_4 = (13!)/(9!4!)`

`^(13)C_4 = (13 * 12 * 11 * 10 * 9!)/(9!4*3*2*1)`

`^(13)C_4 = (13 * 12 * 11 * 10)/(4*3*2*1)`

`^(13)C_4 = (17160)/(24)`

`^(13)C_4 = 715`

`Probability = (Available\ Selection)/(Possible\ Selection)`

`Probability = (350)/(715)`

`Probability = (70)/(143)`