Answer:
It should be 100 days sample so that the margin of error will be 39.2 tons or less
Explanation:
We are given that A coal company wants to determine a 95% confidence interval estimate for the average daily tonnage of coal that it mines.

To Find two tailed critical value using Z table
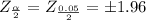
Margin of error = ME = 39.2

Formula :
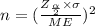
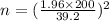
n=100
Hence it should be 100 days sample so that the margin of error will be 39.2 tons or less