Answer:
Rotation frequency is 0.377 hertz.
Step-by-step explanation:
After a careful reading of statement, we need to apply the concept of radial acceleration due to uniform circular motion, whose formula is:
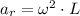 (Eq. 1)
(Eq. 1)
Where:
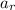 - Radial acceleration, measured in meters per square second.
- Radial acceleration, measured in meters per square second.
 - Angular velocity, measured in radians per second.
- Angular velocity, measured in radians per second.
 - Length of the beam, measured in meters.
- Length of the beam, measured in meters.
Now we clear the angular velocity within:

If
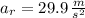 and
and
 , the angular velocity is:
, the angular velocity is:
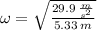
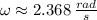
The frequency is the number of revolutions done by device per second and can be found by using this expression:
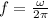 (Eq. 2)
(Eq. 2)
Where
 is the frequency, measured in hertz.
is the frequency, measured in hertz.
If we know that
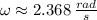 , then rotation frequency is:
, then rotation frequency is:

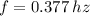
Rotation frequency is 0.377 hertz.