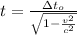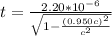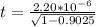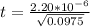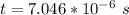Complete Question
The positive
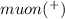 , an unstable particle, lives on average
, an unstable particle, lives on average
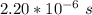 (measured in its own frame of reference) before decaying.
(measured in its own frame of reference) before decaying.
If such a particle is moving, with respect to the laboratory, with a speed of 0.950 c , what average lifetime is measured in the laboratory?
Answer:
The value is
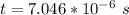
Step-by-step explanation:
From the question we are told that
The the average live time of
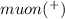 is
is
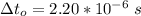
The speed of of
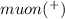 in the laboratory is
in the laboratory is
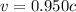
Generally the average life time of the positive
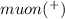 measured in the laboratory is mathematically represented as
measured in the laboratory is mathematically represented as