Question

The derivative of a position function is a velocity function. The derivative of a velocity function is an acceleration function. A particle moves along a straight line. The distance of the particle from the starting point at time t is given by the function: s=t5−6t4 Find the value of t (other than 0 ) at which the acceleration is equal to zero. 6

Answer 1

3.6secs

Step-by-step explanation:

Given the distance of the particle from the starting point at time t is given by the function: s=t⁵−6t⁴

velocity v(t) = ds/dt

`v(t) = 5t^(5-1)-4(6)t^(4-1)\\v(t) = 5t^4-24t^3\\`

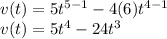
Next is to get the acceleration function:

`a(t) = 4(5)t^(4-1)-3(24)t^(3-1)\\a(t) = 20t^3-72t^2`

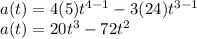
Next is to get the value of t at which the acceleration is equal to zero

`a(t) = 20t^3-72t^2\\0 = 20t^3-72t^2\\20t^3-72t^2 = 0\\t^2(20t-72) = 0\\t^2 =0 \ and \ 20t-72 = 0`

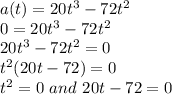
Since t ≠ 0, hence;

20t -72 = 0

20t = 72

t = 72/20

t = 3.6secs

Hence the value of t (other than 0 ) at which the acceleration is equal to zero is 3.6secs