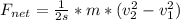Complete Question
The kinetic energy K of an object of mass m moving at a speed v is defined as . It seems reasonable to say that the speed of an object--and, therefore, its kinetic energy--can be changed by performing work on the object. In this problem, we will explore the mathematical relationship between the work done on an object and the change in the kinetic energy of that object.
Let us now consider the situation quantitatively. Let the mass of the sled be m and the magnitude of the net force acting on the sled be The sled starts from rest.
Consider an interval of time during which the sled covers a distance s and the speed of the sled increases from v_1 to v_2. We will use this information to find the relationship between the work done by the net force (otherwise known as the net work) and the change in the kinetic energy of the sled.
Find the net force acting on the sled.
Express your answer in terms of some or all of the variables m,s,
 , and v_2.
, and v_2.
Answer:
The expression is
Step-by-step explanation:
From the question we are told that
The net force is

The distance is s
The first velocity is

The second velocity is

The mass is m
Generally the work energy theorem is mathematically represented as
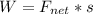
Also from the law energy conservation workdone is mathematically represented as
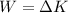
Here
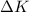 is the change in kinetic energy and this is mathematically represented as
is the change in kinetic energy and this is mathematically represented as
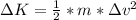
So
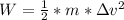
Here
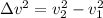
Hence
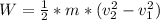
So
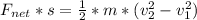
=>