Answer:
Selling 40 items will produce a maximum profit.
Explanation:
We need to use First and Second Derivative Tests on profit function to determine how many items will lead to maximum profit. Let
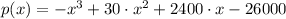 , where
, where
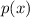 is the profit for a product, measured in US dollars, and
is the profit for a product, measured in US dollars, and
 is the amount of items, dimensionless.
is the amount of items, dimensionless.
First we derive the profit function and equalize it to zero:
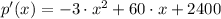
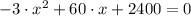 (Eq. 1)
(Eq. 1)
Roots are found by Quadratic Formula:
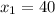 and
and
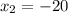
Only the first root may offer a realistic solution. The second derivative of the profit function is found and evaluated at first root. That is:
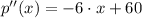 (Eq. 2)
(Eq. 2)
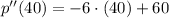
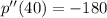 (Absolute maximum)
(Absolute maximum)
Therefore, selling 40 items will produce a maximum profit.