Question

IQ scores have a mean of 100 and a standard deviation of 15. Kate has an IQ of 121. (a) What is the difference between Kate's IQ and the mean

Answer 1

(a) The difference between Kate's IQ and the mean is 21

(b) The z score is 1.4

Explanation:

Here is the complete question:

IQ scores have a mean of 100 and a standard deviation of 15. Kate has an IQ of 121. (a) What is the difference between Kate's IQ and the mean (b) Convert Kate's IQ score to a z score.

Explanation:

(a) To determine the difference between Kate's IQ and the mean, this can be done by subtracting the mean from Kate's IQ.

Mean = 100

Kate's IQ = 121

Difference between Kate's IQ and the mean = 121 - 100 = 21

Hence, the difference between Kate's IQ and the mean is 21.

(b) To convert Kate's IQ score to a z score,

z score is given by the formula

`z =(x - \mu)/(\sigma)`

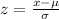
Where
`x` is the score

`\mu` is the mean

and
`\sigma` is the standard deviation

From the question,

`x` = 121

`\mu` = 100

`\sigma` = 15

Then, the z score is

`z =(x - \mu)/(\sigma)`

`z =(121 - 100)/(15)`

`z =(21)/(15)`

`z =(7)/(5)`

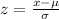
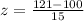
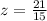
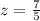
z = 1.4

Hence, the z score is 1.4.