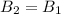Complete Question
The complete question is shown on the first uploaded image
Answer:
The correct option is option 3
Step-by-step explanation:
From the question we are told that
The diameter of solenoid 1 is
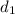
The length of solenoid 1 is
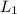
The number of turns of solenoid is
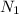
The diameter of solenoid 2 is

The length of solenoid 2 is

The number of turns of solenoid 2 is

Generally the magnetic in a solenoid is mathematically represented as
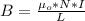
From this equation we see that
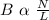
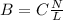
Here C stands for constant
=>
![C = \frac{B * (L)/(N)]()
=>
![\frac{B_1 * (L_1)/(N_1) = \frac{B_2 * (L_2)/(N_2)]()
=>
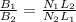
=>
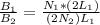
=>
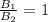
=>