Question

. (Use equations not the psychrometric chart) The dry- and wet-bulb temperatures of atmospheric air at 95 kPa are 25 and 17oC, respectively. Determine (a) the specific humidity, (b) the relative humidity, and (c) the dew-point temperature

Answer 1

a) The specific humidity of air is
`9.774* 10^(-3)\,(kg\,H_(2)O)/(kg\,DA)`.

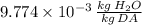b) The specific humidity of air is 0.464.

c) The dew-point temperature is 12.665 ºC.

Step-by-step explanation:

a) The temperature of atmospheric air is considered the dry-bulb temperature, whereas the temperature of entirely saturated air is the the wet-bulb temperature. Dry bulb pressure is the atmospheric air. First we need to find the specific humidity at wet bulb temperature (
`\omega_(wb)`), measured in kilograms of water per kilogram of dry air:

`\omega_(wb) = (0.622\cdot P_(wb))/(P_(db)-P_(wb))` (Eq. 1)

Where:

`P_(wb)` - Wet bulb pressure, measured in kilopascals.

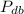`P_(db)` - Dry bulb pressure, measured in kilopascals.

Wet bulb pressure is the saturation pressure of water evaluated at wet bulb temperature, while dry bulb pressure in the pressure presented on statement. If
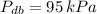`P_(db) = 95\,kPa` and
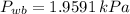`P_(wb) = 1.9591\,kPa`, then the specific humidity at wet bulb temperature is:

`\omega_(wb) = (0.622\cdot (1.9591\,kPa))/(95\,kPa-1.9591\,kPa)`

`\omega_(wb) = 0.0131\,(kg\,H_(2)O)/(kg\,DA)`

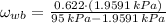
Now we use the following equation to determine the dry bulb specific humidity (
`\omega_(db)`), measured in kilograms of water per kilogram of dry air:

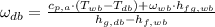`\omega_(db) = (c_(p,a)\cdot (T_(wb)-T_(db))+\omega_(wb)\cdot h_(fg,wb))/(h_(g,db)-h_(f,wb))` (Eq. 2)

Where:

`c_(p,a)` - Isobaric specific heat of air, measured in kilojoules per kilogram-Celsius.

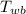`T_(wb)` - Wet-bulb temperature, measured in Celsius.

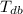`T_(db)` - Dry-bulb temperature, measured in Celsius.

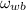`\omega_(wb)` - Wet-bulb specific humidity, measured in kilograms of water per kilogram of dry air.

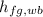`h_(fg,wb)` - Wet-bulb specific enthalpy of vaporization of water, measured in kilojoules per kilogram.

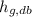`h_(g,db)` - Dry-bulb specific enthalpy of saturated vapor, measured in kilojoules per kilogram.

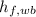`h_(f,wb)` - Wet-bulb specific enthalpy of liquid vapor, measured in kilojoules per kilogram.

If we know that
`T_(wb) = 17\,^(\circ)C`,
`T_(db) = 25\,^(\circ)C`,
`c_(p,a) = 1.005\,(kJ)/(kg\cdot ^(\circ)C)`,
`\omega_(wb) = 0.0131\,(kg\,H_(2)O)/(kg\,DA)`,
`h_(fg, wb) = 2460.6\,(kJ)/(kg)`,
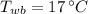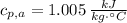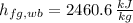`h_(g,db) = 2546.5\,(kJ)/(kg)` and
`h_(f,wb) = 71.355\,(kJ)/(kg)`, the dry bulb specific humidity is:

`\omega_(db) = (\left(1.005\,(kJ)/(kg\cdot ^(\circ)C) \right)\cdot (17\,^(\circ)C-25\,^(\circ)C)+\left(0.0131\,(kg\,H_(2)O)/(kg\,DA) \right)\cdot \left(2460.6\,(kJ)/(kg) \right))/(2546.5\,(kJ)/(kg)-71.355\,(kJ)/(kg) )`

`\omega_(db) = 9.774* 10^(-3)\,(kg\,H_(2)O)/(kg\,DA)`

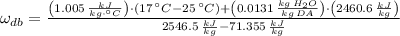
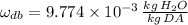
The specific humidity of air is
`9.774* 10^(-3)\,(kg\,H_(2)O)/(kg\,DA)`.

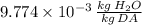b) Then, the relative humidity of air (
`\phi_(db)`), dimensionless, is obtained from this expression:

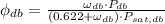`\phi_(db) = (\omega_(db)\cdot P_(db))/((0.622+\omega_(db))\cdot P_(sat, db))` (Eq. 3)

Where
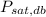`P_(sat, db)` is the saturation pressure at dry-bulb temperature, measured in kilopascals.

If we know that
`\omega_(db) = 9.774* 10^(-3)\,(kg\,H_(2)O)/(kg\,DA)`,
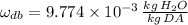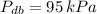`P_(db) = 95\,kPa` and
`P_(sat, db) = 3.1698\,kPa`, the relative humidity of air is:

`\phi_(db) = (\left(9.774* 10^(-3)\,(kg\,H_(2)O)/(kg\,DA) \right)\cdot (95\,kPa))/(\left(0.622+9.774* 10^(-3)\,(kg\,H_(2)O)/(kg\,DA)\right)\cdot 3.1698\,kPa)`

`\phi_(db) = 0.464`

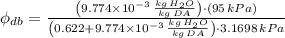
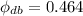
The specific humidity of air is 0.464.

c) The dew point temperature is the temperature at which water is condensated when air is cooled at constant pressure. That temperature is equivalent to the saturation temperature at vapor pressure (
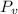`P_(v)`), measured in kilopascals:

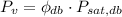`P_(v) = \phi_(db) \cdot P_(sat, db)` (Eq. 4)

(
`\phi_(db) = 0.464`,
`P_(sat, db) = 3.1698\,kPa`)

`P_(v) = 0.464\cdot (3.1698\,kPa)`

`P_(v) = 1.4707\,kPa`

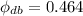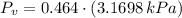
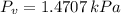
The saturation temperature at given vapor pressure is:

`T_(dp) = 12.665\,^(\circ)C`

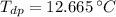
The dew-point temperature is 12.665 ºC.