Answer:
Some coordinate (x, y)
Step-by-step explanation:
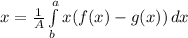
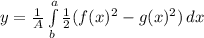
Those are the equations to find a centroid. Let's find the equation that defines the semicircle:
(usual circle, 1 is the radius)
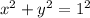
(this will give us our semicircle)
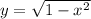
In the equation above, the difference between functions can be defined as a single function if we have no more than one.
Now all you need is to find the roots and compute the integrals.