Question

For a sample of 48 finance majors, the average time spent reading each issue of the campus newspaper is 19.7 minutes, with a standard deviation of 7.3 minutes. The corresponding figures for a sample of 40 management information system majors are 16.3 and 4.1 minutes. What is the the test statistic, t, with the 0.01 level of significance?

Answer 1

The t-value is ±2.626.

Explanation:

An independent sample t-test will be performed to determine whether there is a difference between the average time spent reading each issue of the campus newspaper by finance majors and management majors.

The hypothesis can be defined as follows:

H₀: There is no difference between the two means, i.e.
`\mu_(1)-\mu_(2)=0`

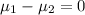
Hₐ: There is no difference between the two means, i.e.
`\mu_(1)-\mu_(2)\\eq0`

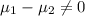
The test statistic is:

`t=\frac{\bar x_(1)-\bar x_(2)}{S_(p)*\sqrt{(1)/(n_(1))+(1)/(n_(2))}}`

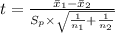
The degrees of freedom is:

`df=n_(1)+n_(2)-2\\=48+40-2\\=86`

The critical value of t is:

`t_{\alpha /2, (n_(1)-n_(2)-2)}=t_(0.01/2, 86)=\pm2.626`

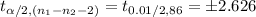
*Use a t-table.

**Use the next higher degrees of freedom if 86 is not available.