Question

Ethan is 1.85 meters tall. At 10 a.m., he measures the length of a tree's shadow to be 28.45 meters. He stands 24.3 meters away from the tree, so that the tip of his shadow meets the tip of the tree's shadow. Find the height of the tree to the nearest hundredth of a meter.  ​

Answer 1

12.68 m (nearest hundredth)

Explanation:

Similar Triangle Theorem

If two triangles are similar, the ratio of their corresponding sides is equal.

Smaller triangle

• height = Ethan's height = 1.85 m
• base = 28.45 m - 24.3 m = 4.15 m

Larger triangle

• height = height of tree = h m
• base = 28.45 m

Ratio of height to base:

`\implies \sf height_(small):base_(small)=height_(large):base_(large)`

`\implies \sf 1.85:4.15=h:28.45`

`\implies \sf (1.85)/(4.15)=(h)/(28.45)`

`\implies \sf h= (1.85)/(4.15) \cdot 28.45`

`\implies \sf h=12.68\:m \:\:(nearest\:hundredth)`

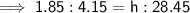
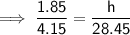
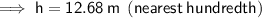
Therefore, the height of the tree to the nearest hundredth of a meter is 12.68 m.

Answer 2

• 12.68 m

Explanation:

Use the similarity of two triangles.

The ratio of corresponding sides is equal.

Let the height of the tree is x, then we have:

• x / 1.85 = 28.45 / (28.45 - 24.3)
• x / 1.85 = 28.45 / 4.15
• x = 1.85*28.45 / 4.15
• x = 12.68 m (rounded)