Question

Thelma and Louise ending filmed at: Dead Horse Point , Moab Utah

Cliff Height: 609.6 m ( 2000 feet)
Vehicle Velocity at cliff edge: 40.3 meters/second (90 miles per hour)
Questions to answer: The Colorado River is at the bottom of the cliff approximately 536.5 meters (1,760 feet) from cliff base. The river averages 300 feet across and is forty feet deep.
A. Does the car land in the river?
B. How much closer to the cliff base would the river have to be, to allow the car to land 50 feet from the edge of the river?​

Answer 1

A. The car does not land in the river

B. 399.27 meters

Step-by-step explanation:

The Cliff Height, s: 609.6 m

The velocity at the edge of the cliff, vₓ = 40.3 meters/second (90 miles per hour)

The location of the Colorado River = 536.5 meters (1,760 feet) from the cliff base

The width of the river across = 300 feet average

The depth of the river = 40 feet

Assumption;

The direction of the vehicle = Horizontal

Vertical velocity of the vehicle = 0 m/s

The time, t, it takes the car to reach the level of the bottom of the cliff is given as follows;

s =
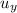`u_y`·t + 1/2·g·t²

Where;

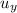`u_y` = The initial vertical velocity of the vehicle = 0

g = The acceleration due to gravity = 9.81 m/s²

Therefore, we have;

609.6 = 0×t + 1/2 × 9.81 × t²

609.6 = 1/2 × 9.81 × t²

t = √(2 × 609.6/9.81) ≈ 11.148 seconds

The horizontal distance, x, travelled by the car in the above calculated, 11.148 seconds, time is x = vₓ × t = 40.3 × 11.148 = 449.27 meters

Therefore, the horizontal distance from the cliff travelled by vehicle on landing from the base of the cliff = 449.27 meters

Given the river is located approximately 536.5 meters from cliff's base, the car does not land in the river

B. In order for the car to land 50 ft. from the edge of the river, the river has to be 449.27 - 50 ≈ 399.27 meters from the base of the cliff.